Son algoritmos algebraicos cuya aplicación simplifica y sistematiza la resolución de muchas operaciones habituales. También reciben este nombre las multiplicaciones con expresiones algebraicas que cumplen ciertas reglas.
Adjunto un vídeo muy completo sobre Productos Notables.
Factor Común
Es el resultado de multiplicar un binomio a+ b por un termino c se obtiene aplicando la propiedad distributiva:
c(a+b)= ca+cb
Ejemplo:
Cuadrado de Un Binomio
Para elevar un binomio al cuadrado (es decir, multiplicarlo por si mismo), se suman los cuadrados de cada termino con el doble del producto de ellos. Así:
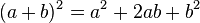
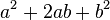Se reconoce una T.C.P (Trinomio Cuadrado Perfecto) cuando su primer y tercer termino son positivos, y cuando el segundo termino es la raiz cuadrada del primer y tercer termino. Producto de dos binomios con un término común
Para resolver un binomio con término común, se tiene que identificar el termino común, en este caso X la cual elevamos al cuadrado, más la suma de los términos no comunes (a)(b). El resultado se multiplica por X más la multiplicación de los no comunes.
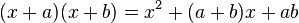
Ejemplo:
Adjunto este cuadro que nos muestra cada una de las expresiones algebraicas.
Producto notable
|
Expresión algebraica
|
Nombre
| |
(a + b)2
|
=
|
a2 + 2ab + b2
|
Binomio al cuadrado
|
(a + b)3
|
=
|
a3 + 3a2b + 3ab2 + b3
|
Binomio al cubo
|
a2 - b2
|
=
|
(a + b) (a - b)
|
Diferencia de cuadrados
|
a3 - b3
|
=
|
(a - b) (a2 + b2 + ab)
|
Diferencia de cubos
|
a3 + b3
|
=
|
(a + b) (a2 + b2 - ab)
|
Suma de cubos
|
a4 - b4
|
=
|
(a + b) (a - b) (a2 + b2)
|
Diferencia cuarta
|
(a + b + c)2
|
=
|
a2 + b2 + c2 + 2ab + 2ac + 2bc
|
Trinomio al cuadrado
|
Producto de dos binomios conjugados
El producto de dos binomios conjugado se diferencia por el signo. Para su multiplicación es necesario elevar los monomios al cuadrado y restarlos.
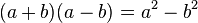
Ejemplo:
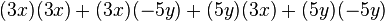
Agrupando términos:
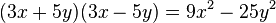
En los siguientes link que adjunto podrán encontrar diferentes ejercicio sobre productos notables resueltos.
Taller
1. (f+12)2
2. (18+2m)2
3. (8a+10b)2
4.(4x-8y)2
5. (5a3- 8b4)2
6. (10x3- 9xy5)2
En este link encontraran un pequeño examen sobre Producto Notable, es para que prueben sus conocimientos. Es muy sencillo, los invito a que lo realicen.
https://docs.google.com/forms/d/1vrzBOQyeOYZoAhqxhwy9VwvfUrROwNjO6WMRBtQsgvY/viewform
En este link encontraran un pequeño examen sobre Producto Notable, es para que prueben sus conocimientos. Es muy sencillo, los invito a que lo realicen.
https://docs.google.com/forms/d/1vrzBOQyeOYZoAhqxhwy9VwvfUrROwNjO6WMRBtQsgvY/viewform
No hay comentarios:
Publicar un comentario